數值電磁 - 電容模擬器自己寫 (part1/3)
此篇紀錄使用MATLAB自己寫一個電容模擬器。
利用數值電磁的方法,計算空間電位、空間電場、金屬上電荷、到最後到電容值。
並將計算結果對比商業3D模擬器,Cadence Clarity Capacitance、Ansys Q3D。
文章最後分享我所編寫的MATLAB程式碼。
主要參考文獻,瑞典皇家理工學院(KTH)Stefano Markidis教授的授課講義。
https://canvas.kth.se/files/1412425/download?download_frd=1
計算兩塊金屬之間的電容數值。
首先介紹相關方程
Maxwell Gauss law:
🜄·E = ρ/ε...(1)
接著定義電位φ和E的關係
E = -🜄φ...(2)
將式(2)帶入式(1)
🜄·(-🜄φ) = ρ/ε
若計算的φ空間是純介質(or空氣),也就是source free(ρ=0), 得
-🜄²φ = 0...(3)
式(3)又稱為Laplace Equation。
接著介紹數值方法來算式子(3)
為了方便,用二維x,y帶入式子(3)
-🜄²φ = მ²φ/მx² + მ²φ/მy² = 0...(4)
採用「中央差分方」把討人厭的微分幹掉
მ²φ/მx² ⋍ (φ(x-△x) - 2*φ(x) + φ(x+△x)) /△x²
მ²φ/მy² ⋍ (φ(y-△y) - 2*φ(y) + φ(y+△y)) /△y²
上式中的△x和△y為xy方向的「mesh」,為了方便 ,把xy的mesh都設定成一樣大
△x=△y=h
帶入式(4)
-🜄²φ ⋍ (φ(x-h,y) + φ(x+h,y) + φ(x,y-h) + φ(x,y+h) - 4*φ(x,y))/h² = 0...(5)
接著介紹Jacobi Iteration來算式(5)
把φ(x,y)丟到左邊寫成
φ(x,y) = (φ(x-h,y) + φ(x+h,y) + φ(x,y-h) + φ(x,y+h))/4...(6)
式(6)是本文最核心的主角,數學有些討厭,用物理解釋式(6)就是:
「x,y點的電位 = 左、右、上、下四個點電位的平均(相加再除4)。」
求解問題如下圖,同軸方形波導管。
施加1V在中央金屬M1,0V在外圈金屬M2,我們想求內外金屬之間的電容。
雖然我們要解的是整個空間的電位,但內外金屬電位其實已經給定,分別為1v和0v,又稱為Boundary Condition(B.C.)。
φ(1cm,1cm) = 1...(7)
φ(2cm,2cm) = 0...(8)
不難想像B.C.是必要的存在,否則式(6)永遠都是0。
有了式(6)(7)(8),我們可以不斷的疊代,將1v和0v擴散到整個空間。
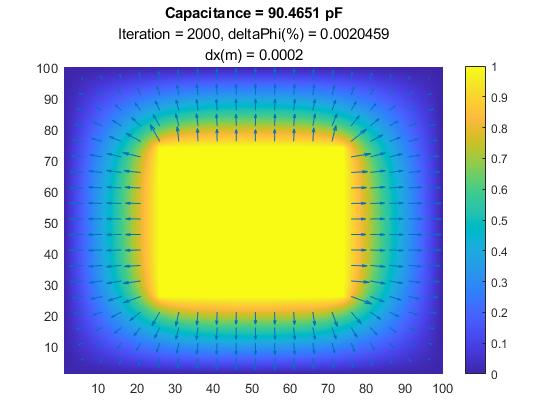
下圖為計算結果,mesh h為0.02cm,疊代2000次。
自製Matlab模擬器(2D),金屬內對外單位電容為90.5pF。
Cadence Clarity Capacitance(3D),金屬內對外單位電容為91.1 pF。
Ansys Q3D(3D),金屬內對外單位電容為91.1pF。
考量到2D和3D solver本質上的差異,這些誤差是可以接受的。
MATLAB模擬結果
電位分布圖
電位等位圖
「MATLAB程式碼 - 方形金屬同軸波導管單位電容器,內圈1cm外圈2cm 」
clc;clear;close all;
%金屬2 cm切100份
meshnum = 100;
dx = 0.02/meshnum; % dx=2cm/100
% Inner Conductor Region
metalsize = round(0.01/dx); % inner metal 1 cm
start = 1+floor((meshnum-metalsize)/2);
endmetal = meshnum - start;
metalregion = zeros(meshnum);
metalregion(start:endmetal,start:endmetal)=1;
% phi Initial guess
phi = rand(meshnum,meshnum); %隨機初始化空間電位
% initial E,D,phi
Ex = zeros(meshnum);
Ey = zeros(meshnum);
Dx = zeros(meshnum);
Dy = zeros(meshnum);
EpsilonMatrix = ones(meshnum);
for nn=1:2000 %疊代次數
phi_before = phi;
for xx=2:1:meshnum-1
for yy=2:1:meshnum-1
% Jacobi iteration of phi for laplace euqation
phi(xx,yy) ...,
= 0.25* ...,
( phi_before(xx-1,yy) ..., % x-1
+ phi_before(xx+1,yy) ..., % x+1
+ phi_before(xx,yy-1) ..., % y-1
+ phi_before(xx,yy+1) ..., % y+1
);
end
end
% set B.C.
% Inner Conductor phi=1
phi(start:endmetal,start:endmetal)=1;
% Outter Conductor phi=0
phi(1,:)=0;
phi(:,1)=0;
phi(end,:)=0;
phi(:,end)=0;
deltaPhi = max(max(abs(phi-phi_before)))*100;
end
% calculate E
Ex(1:end-1,:) = (phi(2:end,:)-phi(1:end-1,:)) /dx;
Ey(:,1:end-1) = (phi(:,2:end)-phi(:,1:end-1)) /dx;
% calculate D
Dx = Ex.*EpsilonMatrix*8.8541878128e-12;
Dy = Ey.*EpsilonMatrix*8.8541878128e-12;
% calculate surface charge density
charge = (sum(abs(Dx(start-1,start-1:endmetal+1))) ...,
+ sum(abs(Dx(endmetal,start-1:endmetal+1))) ...;
+ sum(abs(Dy(start-1:endmetal+1,start-1))) ...,
+ sum(abs(Dy(start-1:endmetal+1,endmetal)))...,
) *dx*1e12; %in pF
% plot potential
figure; contour(phi'); hold on;
quiver(1:5:meshnum,1:5:meshnum,-Ex(1:5:meshnum,1:5:meshnum)',-Ey(1:5:meshnum,1:5:meshnum)'); hold off;
title(['Capacitance = ',num2str(charge), ' pF']);
subtitle({['Iteration = ',num2str(nn), ', deltaPhi(%) = ',num2str(deltaPhi)], ...;
['dx(m) = ',num2str(dx)]});
colorbar;
% plot potential contour
figure; pcolor(phi'); shading interp;hold on;
quiver(1:5:meshnum,1:5:meshnum,-Ex(1:5:meshnum,1:5:meshnum)',-Ey(1:5:meshnum,1:5:meshnum)'); hold off;
title(['Capacitance = ',num2str(charge), ' pF']);
subtitle({['Iteration = ',num2str(nn), ', deltaPhi(%) = ',num2str(deltaPhi)], ...;
['dx(m) = ',num2str(dx)]});
colorbar;



留言
張貼留言