數值電磁 - 電容模擬器自己寫 (part3/3)
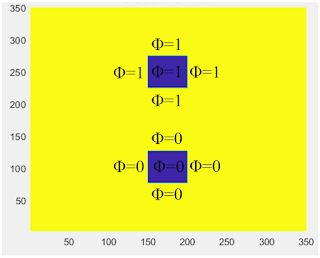
此篇延續[數 值電磁 - 電容模擬器自己寫 (part1/3) ], [ 數值電磁 - 電容模擬器自己寫 (part2/3) ] 用MATLAB寫一個計算電容的數值模擬器，此篇介紹邊界條件Boundary Condition。 1. 如何給電壓值 2. 如何模擬無限大free space [如何給電壓值] 我們知道電容C=Q/△V 若有兩個金屬，一個給1V，另一個給0V。 那麼金屬上會自然感應出電荷Q，而感應電荷的量越多，代表C越大。 那麼1V在模擬上是如何加在金屬上的呢? 前兩篇介紹到Laplace Equation。 -🜄²φ = 0 電壓=電位=φ。 常見電容模擬器會將整個金屬視為等電位。 所以模擬上金屬給1V，只要將整塊金屬的φ都強制設定為1V就可。 如下圖，藍色是金屬，其一金屬φ永遠是1(V)，另一金屬φ永遠是0(V)。 此類型又稱Dirichlet Boundary Condition [如何模擬無限大free space] 前兩篇介紹到Laplace Equation的有限差分型態。 φ(x,y) = (φ(x-h,y) + φ(x+h,y) + φ(x,y-h) + φ(x,y+h))/4 「x,y點的電位 = 左、右、上、下四個點電位的平均(相加再除4)。」 如下圖 剛我們已將中間的金屬強制給定電壓φ=1V或0V。 而其他空間φ(x,y)可由上式算出，由左、右、上、下四個點電位求得。 有趣的是邊界呢? 例如最左邊邊界φ(1,y)，已經沒有更左邊的電位可以用來算φ(1,y)。 例如最下邊邊界φ(x,1)，已經沒有更下的電位可以用來算φ(x,1)。 所以邊界上的φ是必經特別處理的，我們稱為邊界條件(Boundary Condition)。 一種邊界條件處理是不管他(不算他)，讓邊界φ維持為0。 其實仔細思考，這就等同於外面包著一塊0V的金屬(如同 [如何給電壓值] 剛剛描述)。 如下圖，整體架構變成3塊金屬，而最外面那圈的電壓為0v。 不難想像，整體電容值會更大，因為多了金屬到外圈的電容。 顯然把邊界φ維持為0不是個好主意，破壞了原本模擬的架構。 但更經常，我們想知道的是只有2塊金屬單純地放在空氣中(或介質)中。 問題就成為，我們如何用運算「有限大」空間，去得到「無限大」空間的結果。 一種近似方法是 floating
